Maths class, Roman style

Those designing and constructing ancient buildings and other structures had simple tools at their disposal. They made sketches and recorded measurements on wax tablets using a small bronze rod with a pointed end, the so-called stylus. A number of such implements have been discovered in Aquincum as well. Wax tablet fragments were found in Budapest at modern-day Vörösvári Road, inside a well at the edge of the ancient Military Town, as well as at Bécsi Road, in one of the graves of the Military Town’s cemetery. The ‘blueprints’ were presumably drawn on parchment. For making the designs they used bronze pairs of compasses, of which three have been found in Aquincum so far. Two were deposited in graves, while the third was uncovered in the Mithras temple of Symphorus in the Civil Town. For drawing straight lines and constructing right angles and 45-degree angles, they used a cast bronze ruler and protractor. Such an implement was found among the assemblage at Szél Street containing carpentry tools. For checking if something was vertical, they could make use of a plummet and a plumb line. Original pieces can be seen at the Ingenious Inventions – Innovative Ideas temporary exhibition as well as the Visible Storage permanent exhibition of the Aquincum Museum.

Fig. 1. A reconstruction of the desk of a Roman ‘engineer’ with wax tablets, a stylus (writing implement), ruler, plummet and compass (Photo by Nóra Szilágyi)

Calculations were necessary not just when designing and building structures. They were also needed for water usage, at the accountant’s office or in the shop, in all kinds of everyday situations. For calculations the Romans used a counting board called the abacus, a word which came from Greek. Abacus could also mean a table, board or gaming board. Calculations were made originally using small round pebbles, or calculi (plural of calculus) on the counting board. According to Herodotus, the Greeks and Egyptians too used small stones for calculation. The oldest Greek abacus is an incised marble tablet found in 1846 on the island of Salamis from presumably around 300 BC.  From the Roman period we currently know of five abacuses. One is held in Paris, another in Rome – unfortunately their find-spot is unknown – while a third was recovered by an excavation in north Italy, at one of the cemeteries of ancient Augusta Praetoria (modern-day Aosta). This was deposited in a cremation grave – along with an inkwell and styluses – and can be dated to the late 1^st century AD. These abacuses were small (around 12×8 cm) bronze ‘pocket calculators’. We know of two further pieces from descriptions in the modern period. They belonged to the private collections of scholars in Augsburg and Rome in the 17^th century; their later fate, however, is unknown. For the  exhibition at the Aquincum Museum we had a bronze replica made based on the piece held in Paris (Médailles et Antiques de la Bibliothèque nationale de France), which is on display at the Ingenious inventions – Innovative ideas temporary exhibition.

Video 1. Using an abacus made based on the Roman model (in HU with EN subtitles)

The Roman abacus

Roman counting boards were rectangular. In the upper part of the board there are eight short grooves, while in the lower part, on the extant pieces, there are nine long grooves. On the abacuses from Augsburg and Rome, known only from their description, instead of the ninth groove there seem to have been three short notches, one below the other, by the right edge of the board. The numerical values are indicated between the upper and lower series of grooves. From left to the right, the first seven signs (and their Arabic number equivalent) are:

IXI = 1.000.000 (decies centena milia)
(((I))) = 100.000 (centum milia)
((I)) = 10.000 (decem milia)
(I) = 1.000 (mille)
C = 100 (centum)
X = 10 (decem)
I = 1 (unus)

Between the eighth upper and lower groove is the Greek letter theta, which indicates one-twelfth of the whole, i.e. the uncia. The final groove (or notches) can be used to calculate the half, quarter, and third uncia (i.e. 1/24, 1/48, and 1/36).

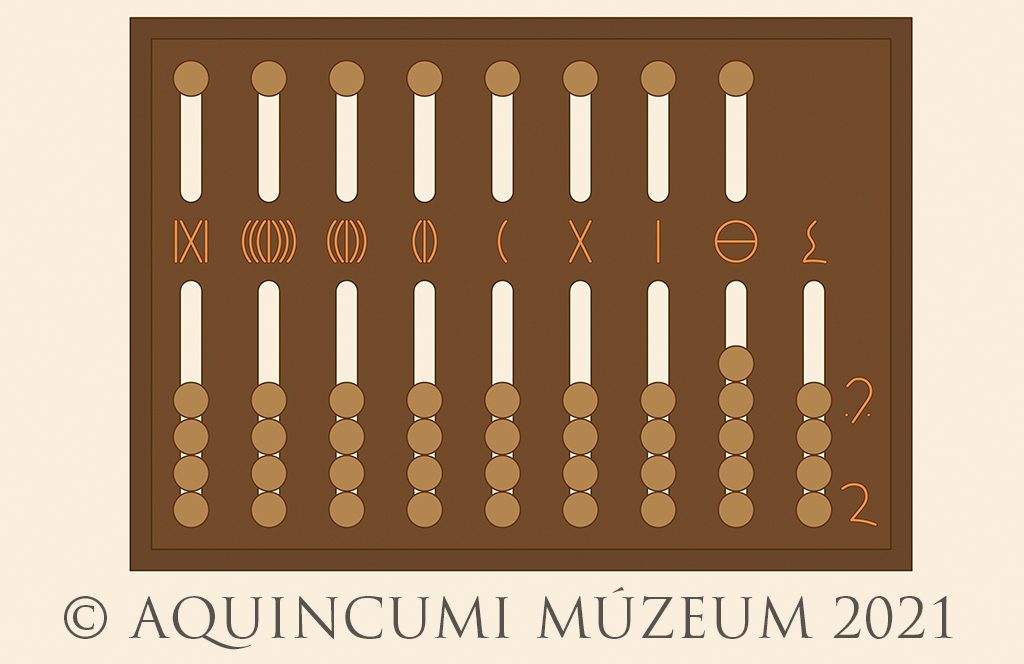
Fig. 2. The layout of the Roman abacus (Drawing by Tamás Lajtos)

Roman abacuses could represent whole numbers up to 9,999,999, while fractions could be represented in the final two grooves. In the grooves they placed little bronze beads, which represented the numerals from 1 to 9. In each lower groove there are four beads; each bead has a value of 1. In each upper groove there is one bead, which has a value of 5. In the eighth lower groove from the left there are five beads, each with a value of 1/12 or one uncia. In the eighth upper groove there is one bead, which is worth six unciae (6/12 of the whole). The last groove on the right can be used for uncia fractions. Here we find four beads. The value of the topmost bead is a half uncia, or 1/24 of the whole. The next bead’s value is a quarter uncia, or 1/48 of the whole. Both beads at the bottom are worth a third unicia each, i.e. 1/36 of the whole. As 1/24 plus 1/24 equals 1/12, or one uncia, it can be marked in the next groove to the left. Similarly, there is only one bead for a quarter uncia, as two quarters of an uncia make a half uncia, which is the value of the bead at the top. We need two of the beads representing one third of an uncia, as 1/36 plus 1/36 equals 2/36, which is not represented by another bead.

Become an ancient engineer!

Let’s calculate with a Roman abacus

Roman counting boards in effect helped keep track of mental calculations. They could be used for addition, subtraction and multiplication. At the start the beads in the lower grooves are pulled down and the beads in the upper grooves are pulled up. We then pull towards the middle the values we need for the calculation. Let’s take an easy example and add 625 and 127. First we mark 625 on the abacus, then – from right to left – we add the ones and mark them on the abacus; then come the tens and then the hundreds. The result is 752. The short video below presents this calculation with the Roman abacus:

Addition with a Roman abacus (in HU with EN subtitles)

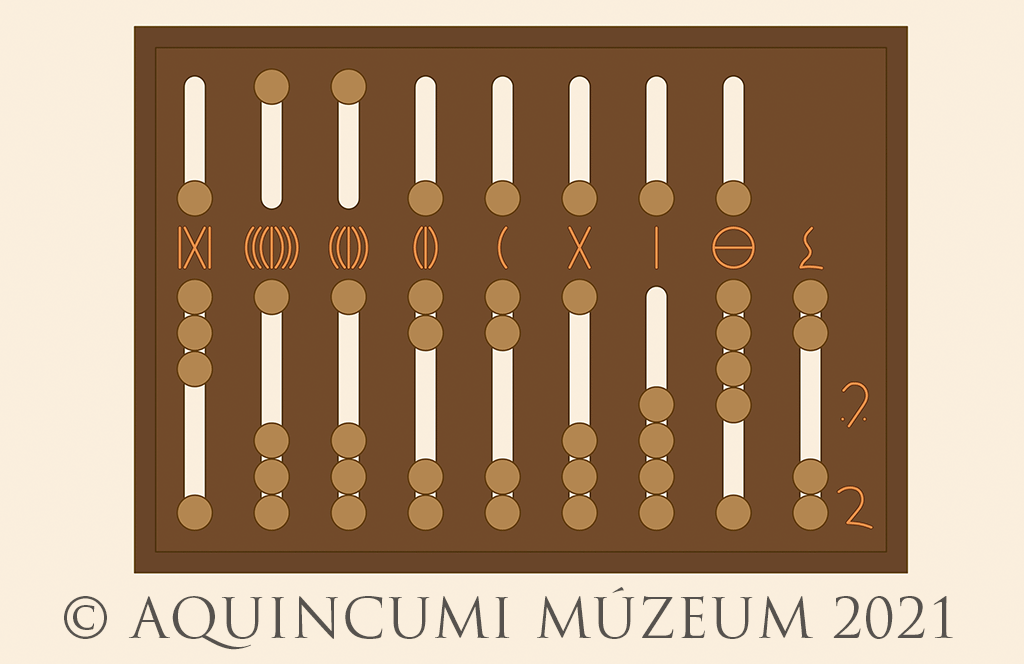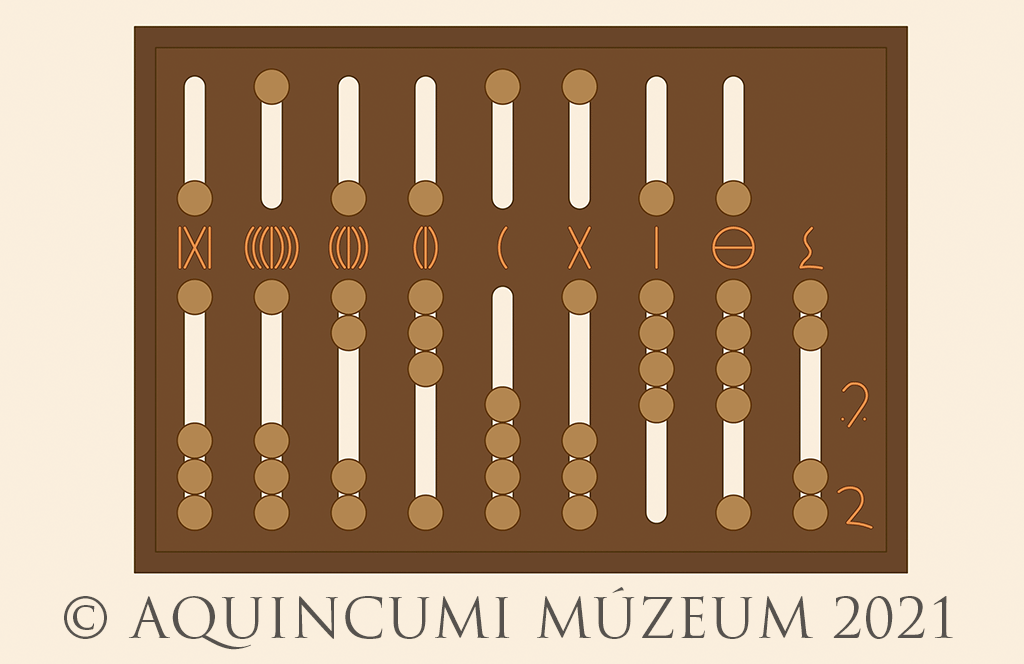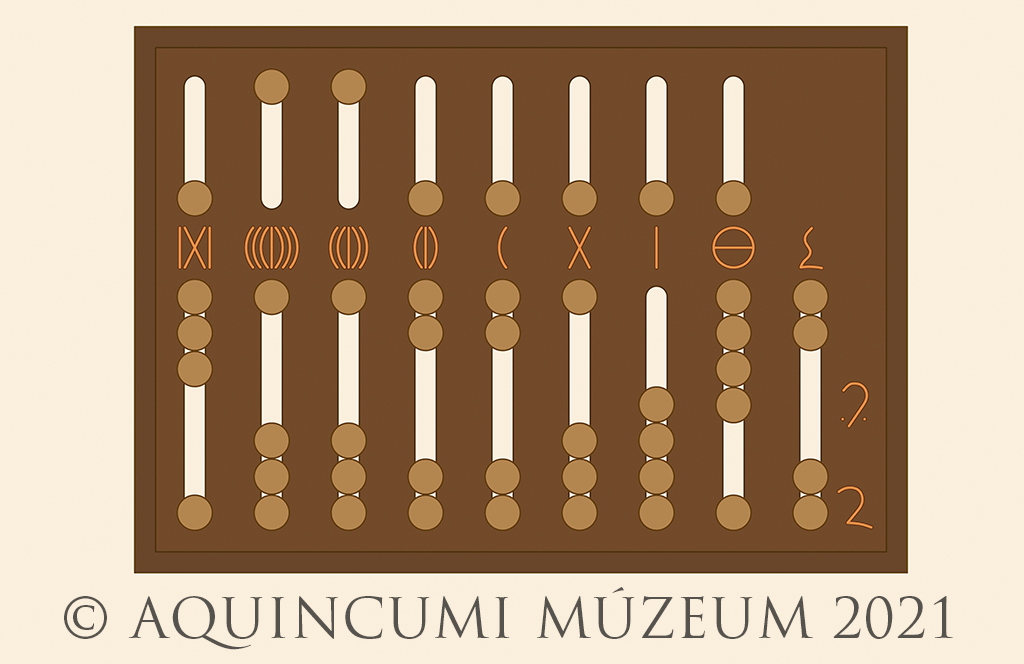
Let’s now take a bigger number! In the image below, we see 6,178,019 as well as ten unciae (10/12), a half uncia (1/24) and a quarter uncia (1/48):

Fig. 3a. Marking 6,178,019 and 43/48 on the abacus (Drawing by Tamás Lajtos, Edited by Krisztián Kolozsvári)

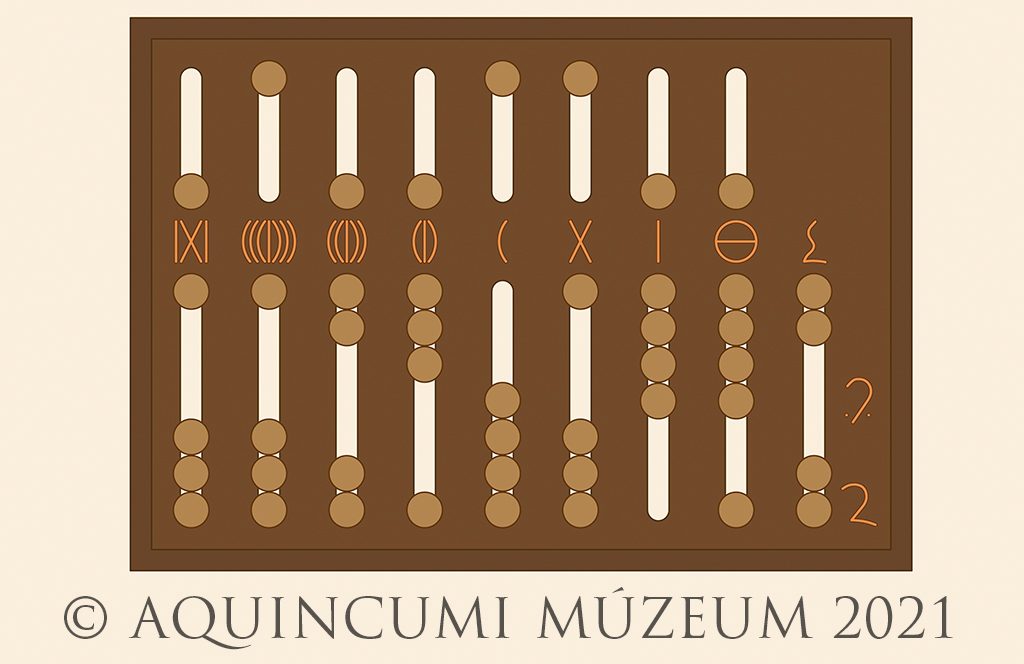
Fig. 3b. 6,178,019 and 43/48 (Drawing by Tamás Lajtos)

Let’s then add to this number 1,939,746. The result can be seen on the abacus of Fig. 4. below (8,117,765 and 43/48 in Arabic numerals).

Fig. 4. The addition and the result: 8,117,765 and 43/48 (Drawing by Tamás Lajtos, Edited by Krisztián Kolozsvári)

For subtraction, we subtract from each other the ones, then the tens, then the hundreds and so on. We mark the partial results on the abacus, and then we can read the final number.

Subtraction with a Roman abacus (in HU with EN subtitles)

If we want to multiply bigger numbers, e.g. of three Arabic digits, using a Roman abacus, we have to break down the numbers into hundreds, tens and ones. We then multiply each of these separately then add the resulting numbers. We can track the partial results on the abacus until we receive the final result. E.g. for 428 x 111:

400×100=40000
20×100=2000+40000=42000
8×100=800+42000=42800
400×10=4000+42800=46800
20×10=200+46800=47000
8×10=80+47000=47080
400×1=400+47080=47480
20×1=20+47480=47500
8×1=8+47500=47508

Multiplication with a Roman abacus (in HU with EN subtitles)

But how did the Romans do division? We don’t know. J. Hilton Turner (Roman elementary mathematics. The Classical Journal 47, 1951, 63-74, 106-108) suggests the following method:

Let’s divide 808 by 35!

808 can be divided by 35 at least ten times. We subtract 350 and get 458.
458 can be divided by 35 at least ten times. We subtract 350 and get 108.
108 can be divided by 35 at least once. We subtract 35 and get 73.
73 can be divided by 35 at least once. We subtract 35 and get 38.
38 can be divided by 35 at least once. We subtract 35 and get 3.
Therefore 808 can be divided by 35 twenty three times, with a remainder of 3 on the abacus.

Written by Dr Gabriella Fényes

Click here to read the other entries of our online exhibition.